Medição sem Interação

Esta postagem é para quem leva ciência a sério.

A luz tem um comportamento contraditório, pelo menos do ponto de vista da maneira como a percebemos em laboratório. Por um lado ela demonstra ter todas as características de uma onda, com frequência, comprimento de onda, fase e amplitude perfeitamente mensuráveis. Por outro lado, também demonstra ter uma natureza corpuscular. Há várias evidências disso, como a quantização da energia de qualquer tipo de radiação e a detecção de fótons (o nome que se dá ao quantum de luz) individuais em chapas fotográficas. A aparente contradição se dá pelo fato de que ondas se propagam pelo espaço ao redor da fonte, enquanto partículas deveriam ser incapazes de fazer isso. No entanto, a luz parece ser formada por partículas que de algum modo têm seu comportamento dependente de condições de contorno, mesmo que ela não tenha interação diretamente detectável com tais contornos. A este fenômeno se dá o nome de não-localidade.

Existe uma brincadeira simples que pode ser feita em casa para demonstrar o comportamento contraditório da luz. Se você ligar uma caneta laser e apontar o feixe de luz diretamente para uma parede, fica claro o comportamento corpuscular. Afinal, a luz é emitida pela fonte e atinge um ponto específico da parede, conforme a vontade do usuário. Isso sugere partículas (corpúsculos) emitidas por uma fonte, atingindo uma região muito limitada do espaço. Portanto, não há evidências detectáveis de que a luz do laser esteja se propagando por todo o espaço ao redor, a não ser por pequenos fenômenos de espalhamento devidos à interação dos fótons do laser com partículas de gases e pó entre a fonte e o alvo (parede). Em condições ideais de vácuo, esse espalhamento residual simplesmente não existiria. 

Agora vamos para a próxima etapa da brincadeira, assumindo que seu laser é o mais comum e barato, ou seja, vermelho. Fixe a caneta laser ligada em posição horizontal, sobre uma mesa. Ela deve estar a uma distância de uns quatro metros da parede. No ponto médio, coloque um fio de cabelo no caminho do laser, de modo a dividir a trajetória daquele feixe de luz coerente em dois caminhos: à esquerda do fio de cabelo e à direita. Este é o célebre experimento das duas fendas. Os dois lados do fio de cabelo operam, na prática, como duas fendas ou dois caminhos pelos quais o feixe de laser deve passar simultaneamente.

Agora observe o padrão de luz detectado na parede, dois metros adiante do fio de cabelo. Você perceberá a formação de várias linhas espectrais de luz vermelha. Se a luz tivesse apenas comportamento corpuscular, não haveria mais do que dois pontos luminosos sobre a parede: um correspondente aos fótons que passaram pelo lado esquerdo do fio de cabelo e outro correspondente aos fótons que passaram pelo lado direito. No entanto, o que se observa é algo totalmente diferente: vários pontos de luz à esquerda e vários à direita. A explicação usual para este fenômeno é o comportamento ondulatório da luz. A luz emitida pela fonte do laser é coerente. Isso significa que cada fóton tem o mesmo comprimento de onda e a mesma fase. Quando os fótons passam pelo fio de cabelo, separando seus caminhos em dois, o comprimento de onda não muda, mas a fase se altera. Desta forma, fótons com diferente fases interferem entre si de forma construtiva e destrutiva. Quando ocorre interferência construtiva na parede, percebe-se luz vermelha. Quando ocorre interferência destrutiva, nenhuma luz é detectada. Ou seja, escuridão na parede não significa ausência de fótons. Significa apenas que os fótons que atingiram aquela região estão com uma diferença de fase destrutiva. É o caso em que luz somada à luz gera escuridão. Por isso temos regiões de escuridão alternadas com regiões de luz sobre a parede. Portanto, para explicar a existência de múltiplos pontos de luz, apela-se usualmente ao conceito de onda. 

Tal brincadeira pode ser usada até mesmo como instrumento de medição do diâmetro do fio de cabelo. Conhecendo-se o comprimento de onda da radiação laser e as distâncias entre fonte, fio de cabelo e parede, basta medir as distâncias entre os pontos de luz projetados sobre o alvo e aplicar mecânica ondulatória elementar. Trata-se de um processo de medição muito mais preciso do que o emprego direto de réguas e mera inspeção visual direta.

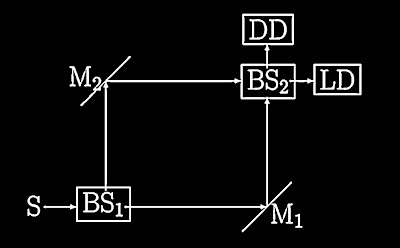
Esta brincadeira, em laboratório, comumente é modificada para um arranjo experimental diferente, mas equivalente. Trata-se do interferômetro de Mach-Zehnder, conforme a figura abaixo, retirada de artigo que fiz anos atrás em parceria com o filósofo Otávio Bueno. 

Na figura, M1 e M2 são, respectivamente, Espelho 1 e Espelho 2. BS1 e BS2 são semi-espelhos (1 e 2), com eficiência de 50%. Isso significa que qualquer fóton que atinja um dos semi-espelhos terá 50% de chances de ser refletido e 50% de chances de seguir adiante. LD e DD são chapas fotográficas. A posição dos espelhos, dos semi-espelhos e das chapas fotográficas é feita de tal modo que LD receba apenas fótons com interferência construtiva e DD receba apenas fótons com interferência destrutiva. Na prática isso significa que qualquer fóton emitido pela fonte S deve ser detectado 100% das vezes na chapa LD e jamais na chapa DD. Ou seja, o primeiro semi-espelho opera como o fio da cabelo na brincadeira acima. Já os espelhos e o segundo semi-espelho têm a função de coordenar a separação entre interferências construtivas e destrutivas. 

Pois bem. Agora vamos a um aspecto mais bizarro ainda do interferômetro de Mach-Zehnder. No início dos anos 1990 os físicos Avshalom Cyrus Elitzur e Lev Vaidman publicaram um resultado inesperado, apesar de aparentemente óbvio. Imagine que você coloque um objeto opaco no caminho entre BS1 e M2. Uma vez que o primeiro semi-espelho opera como um separador de caminhos (analogamente ao fio de cabelo do início deste texto), este objeto funciona simplesmente como uma obstrução de um dos caminhos. Com esta obstrução, qualquer fóton emitido pela fonte S de luz coerente está fadado a jamais encontrar interferência no caminho, seja destrutiva ou construtiva. Portanto ele terá comportamento exclusivamente corpuscular. Isso significa que as chances de ele ser detectado na chapa LD se reduzem a 50%. Analogamente, as chances de ser detectado na chapa DD sobem de zero para 50%. 

O que se infere disso tudo? 

Considere que o tal do objeto opaco é uma bomba sensível à luz: basta um fóton incidente para fazê-la explodir. Imagine agora que o físico experimental emita um fóton de luz coerente a partir de S. Existem três possibilidades: 

(i) o fóton é refletido por BS1 e faz a bomba explodir; 

(ii) o fóton passa direto por BS1 e é posteriormente detectado em LD; 

(iii) o fóton passa direto por BS1 e é posteriormente detectado em DD. 

Nas duas últimas possibilidades a bomba não explode. Mas é justamente a terceira possibilidade que desperta a atenção dos físicos. Isso porque qualquer fóton detectado em DD (a chapa na qual não se espera detecção de fóton algum, no caso do interferômetro estar com todos os caminhos desobstruídos) denuncia a existência de algum objeto opaco dentro do interferômetro. O fóton detectado em DD é o negativo de uma foto de um ponto específico da bomba. Isso significa que é possível fotografar uma bomba sensível à luz sem explodi-la. Temos, portanto, uma medição sem interação. Medição no sentido de detectarmos parte do contorno de um objeto opaco. Sem interação no sentido de que não incide um único fóton detectável sobre ele. 

Vale observar que esta medição espacial tem sérias restrições métricas. Isso porque ela não permite dizer onde está o tal do objeto opaco. Ele pode estar entre BS1 e M2, entre BS1 e M1 ou entre M2 e BS2. Ou seja, temos aqui uma experiência que denuncia a estrutura topológica do toróide cortado definido pelo interior do interferômetro (quando o objeto opaco está lá dentro), mas não a sua estrutura métrica. Até onde sei, é a primeira vez que esta conclusão é publicada em algum lugar: neste blog.

A eficiência de medição do objeto opaco através de detecção de fótons na chapa DD é pequena. Apenas em 25% das vezes em que o experimento é executado podemos ter certeza de que há uma bomba fotossensível no interior do interferômetro sem explodi-la. No entanto, posteriormente este experimento foi aperfeiçoado usando o chamado efeito Zenão quântico. Até a época em que acompanhei a literatura especializada, havia registro de fotografias de objetos macroscópicos com esta técnica, atingindo uma eficiência acima de 80%. Teoricamente essa eficiência pode ser tão próxima de 100% quanto quisermos.

Na última vez em que estive nos Estados Unidos, fiz uma generalização deste arranjo experimental para ondas materiais. O trabalho foi feito em parceria com o filósofo brasileiro Otávio Bueno. 

Ondas materiais são formadas por partículas materiais como elétrons, nêutrons, átomos ou mesmo moléculas. Isso porque fótons não são as únicas partículas com comportamento ondulatório. Componentes de matéria também contam com a dualidade onda-partícula. 

Mas a interferometria de ondas materiais é muito mais ardilosa. Isso porque ela não pode contar com instrumentos óticos para a sua observação. O instrumento que usamos em nosso experimento hipotético é o chamado interferômetro de Mach-Zehnder de três grades, conforme a Figura abaixo.

No lugar de espelhos ou semi-espelhos temos grades de cristal, membranas de difração nanofabricadas ou as conhecidas laser standing waves. Tais grades não dividem os possíveis caminhos em apenas dois, mas em várias ordens de divergência. Além disso, com a única exceção da interferometria de elétrons concebida por Akira Tonomura, partículas materiais não podem ser emitidas individualmente. Há limitações tecnológicas consideráveis. Por isso nossa proposta ainda deve aguardar um bom número de anos até ser realizável na prática. Mas o que Bueno e eu propomos em artigo publicado na americana Foundations of Physics Letters é uma técnica que permite, entre outras coisas, detectar campo elétrico sem perturbação alguma em qualquer carga-prova. 

O que Bueno e eu fizemos foi estender a medição sem interação de Elitzur e Vaidman para objetos físicos que não sejam apenas objetos opacos. Ou seja, estendemos a proposta para a detecção de campos elétricos e magnéticos. Até mesmo para campos gravitacionais discutimos sobre um possível arranjo experimental. 

Do ponto de vista filosófico a medição sem interação ainda precisa qualificar com maior precisão o que, afinal de contas, é interação. Renato Angelo, do Departamento de Física da Universidade Federal do Paraná, tem procurado responder a essa questão. Do ponto de vista matemático, a dissociação física da estrutura topológica do espaço é algo que também precisa ser melhor compreendida. 

Isso significa que esta postagem oferece ao jovem brasileiro uma perspectiva real de pesquisa futura. Neste contexto apresento abaixo mais uma sugestão ao jovem pesquisador.

Definir de maneira matematicamente precisa o que é não-localidade em mecânica quântica. Vejo muitas definições absurdas para não localidade. A única visão sensata que consigo admitir é a seguinte: um sistema quântico de duas ou mais partículas é não-local se, e somente se, ele não puder ser dividido em subsistemas não triviais. 

Para colocar em prática a tradução desta visão em termos matematicamente precisos vejo apenas uma única maneira: axiomatizar de forma sensata a mecânica quântica. 

Por axiomatização sensata da mecânica quântica entende-se o seguinte: um predicado conjuntista que traduza da forma mais fiel possível tudo aquilo que se sabe de mais relevante sobre os fatos experimentais da mecânica quântica.

Sobre predicados conjuntistas devo escrever em breve neste blog.